


Next: About this document ...
Statistics 101: Midterm Exam 1
Problem I
- A.
- Since the distance from the median to lower quartile
Q1 is less than the distance from the median to the upper
quartile Q3 this indicates the number of hits is skewed to the
right. Also the lower whisker is smaller than the upper whisker.
- B.
- Visually 36 is not above the upper whisker.
Also
IQR=Q3-Q1=19-2=17 and the upper inner fence is
Q3+1.5*IQR=44.5. Since 36 is smaller it is not a candidate
outlier.
- C.
- The median is higher for recreational than for
business. Since the box is bigger for recreational it also has
higher variance. Business and recreational are both skewed to the
right.
- D.
- Since 36 is well above the box for business it would
be candidate outlier. Visually
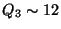 and
and
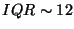 .
So
limit is
12+1.5*12=30.
.
So
limit is
12+1.5*12=30.
- E.
- (i)
- The right tail would be pulled in (higher values
less extreme). This would make the data look symmetric.
- (ii)
- Since logs preserve order, median of the
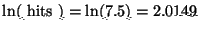 .
.
Problem II
- A.
- Because B and C are independent, it follows
that
- B.
- Since
 is a subset of
is a subset of 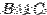 we get that
we get that
- C.
- (i)
- Since
 we find that
we find that
The different interpretation of this question is possible, so the
full credit is granted also for the following solution:
- (ii)
- Since the probability that C occurs is independent
of whether A or B occurs we have that
Hence,
Problem III
- A.
-

- B.
- Using previous result we find that
- C.
- The probability of finding the page on A is .5; for
B this probability is .56; for C it is .63. So search engine C is
best.
- D.
- First we note that
So,
Problem IV
- A.
- The probability distribution of X is shown below:
| X |
-1000 |
0 |
500 |
1000 |
 |
.1 |
.2 |
.2 |
.5 |
- (i)
-

- (ii)
-
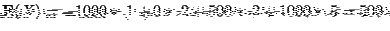
- (iii)
-
 Respectively, standard deviation
Respectively, standard deviation
 .
.
- B.
- (i)
-

- (ii)
-

- C.
- The distribution of daily profits, Y, is given by
| Y |
-1500 |
-500 |
500 |
1500 |
 |
.1 |
.2 |
.2 |
.5 |
Hence,




Next: About this document ...
Wenxin Mao
1999-10-13




