Statistics 101: Homework 1

Exercise 2.2

The task here is to interpret the histogram rather to construct it.

a.

The average value falls in the middle of the histogram, where the histogram balances. This particular histogram is close to symmetric; with nearly equal left and right tails. It appears to us that the histogram would balance somewhere in the interval between 842 and 847. Therefore the average value should be about 845.

Variability is a matter of how spread out the histogram is. In this case, there is a value in the 812 to 817 interval, and, on the other side, a value in the 867 to 872 interval. (Note in both intervals, the frequency is shown as 1, so there is only one value.) We'd say there was virtually no skewness.

b.

The smoothed component is shown as a curve through the histogram. Skewness is indicated by a nonsymmetric curve. In this case, the curve appears almost perfectly symmetric around the middle peak. There is a little or no skewness.

Exercise 2.3

Recall that a stem-and-leaf display, like the one shown, groups the data according to the values in the stem. The first value shown must be 812 (as opposed to 81.2 or 8120), from a look at the data.

The stem-and-leaf display gives interval width of 10, in contrast to the width of 5 in the histogram. In effect, the stem-and-leaf display centers the intervals at 815, 825, etc.; the centers for the histogram also differ. The two pictures aren't identical.

We see basically the same pattern in both displays. The average value is somewhere in the 840's, there is modest variability, and there is very little skewness.

Exercise 2.11

a.

The mode is defined to be the most common value, and is most often used to describe qualitative data. Here, the data are quantitative. The mode is not very useful for such data.

b.

The median is defined as the (n+1)/2th value, when the data are arranged from lowest to highest. There are n=26 data values; the median is the (26+1)/2=13.5th value, the average of the 13th and 14th values. Arrange the data in order from low to high.

547	625	630	656	664	667	667	667	679	688	688	688	688
688	691	694	697	699	700	701	702	703	703	703	708	711

c.

The mean is the average of all 26 numbers. We would regard the data as a sample from the ongoing production process, so we would call the mean $\bar{y}$. Of course, it doesn't matter if we had the original number, or the sorted numbers.

$$\bar{y}=\frac{546+625+\cdots+711}{26}=679.4$$

d.

Remember that the mean is pulled in the direction of skewness, as compared to the median. Here, the mean is less than the median, indicating that there is a ``tail'' of data toward the left ( smaller) values, pulling the mean down relative to the median.

Exercise 2.12

Recall that the first digit(s) of each data value are recorded in the the left-hand, stem part of the diagram, and the next digit in the right hand, leaf part. It's easiest to use the sorted data, but either way gives the same picture. The 547 value is far lower than any other, so we might indicate it separately.

54	7
63	5
63	0
64
65	6
66	4 7 7
67	7 9
68	8 8 8 8 8
69	1 4 7 9
70	0 1 2 3 3 3 8
71	1

The data are clearly left skewed, and there is one outlier on the low (left) side. Even if we to ignore the outlier, there is still skewness.

Exercise 2.17

a.

The mean is shown as 794.23; the standard deviation (STDEV)is shown as 34.25. Therefore, mean minus one standard deviation is 794.23-34.25=759.98 and mean plus one standard deviation is 794.23+34.25=828.48. The actual data are whole numbers, not decimals; values between 760 and 828 will fall in this interval.

b.

51 out of 60 is 85$\%$; 51/60=0.85. According to the Empirical Rule, the percentage theoretically should be only $68\%$. The one standard deviation interval is too wide in this case. It seems likely that skewness or outliers have inflated the standard deviation. This will make the interval ``too wide'' and capture ``too many'' of the data values.

Exercise 2.18

Recall that outliers are shown in a boxplot as points beyond the ``whiskers'' of the plot. The boxplot shows several outliers, including one very serious one. These outliers will inflate the standard deviation, making the ``one standard deviation interval'' wide and causing the Empirical Rule to fail.

Exercise 2.70

b.

A histogram is shown here. The data appear basically mound-shaped, with a modest right skew.

c.

The mode is at 65, which is a decent first guess for the mean. But there are more values higher than 65 than lower. These values will pull up the mean a little. The mean should be a bit above 65, say about 66.

d.

The range $66\pm 5$ just about includes all the values. Therefore, two standard deviations be about 5, so one standard deviation should be about 2.5.

e.

JMP yielded

             FOOD
Minimum              61.22
Maximum              70.74
Mean                 66.02377 
Median               65.81
Standard Deviation        2.114983

Exercise 2.71

a.

A stem-and-leaf display of the data is as follows:

Decimal point is at the colon
   12 : 4
   12 : 99
   13 : 00111222444
   13 : 55556667778889999
   14 : 0011112244
   14 : 5678999
   15 : 0
   15 : 555
   16 : 1

We would call that more or less bell-shaped, with some right skew.

e.

JMP yielded

             NONFOOD
Minimum              12.38
Maximum              16.15
Mean                 13.94585
Median               13.84
Standard Deviation        0.7710269

Exercise 2.72

a.

Here is a boxplot.

b.

There is one candidate outlier on the low side, at about 0.805 or so. There are no outliers shown above the upper whisker.

c.

JMP calculated summary statistics as shown here.

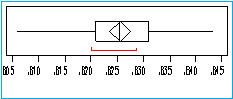
             RATIO
Minimum              0.8060
Maximum              0.8434
Mean                 0.8256
Median               0.8254
Standard Deviation       0.007367554

Is it true that 0.8256=66.02377/(66.02377+13.94585)? By hand, the fraction comes out to 0.8256, all right. In fact, it isn't true in general that the mean of a ratio is the ratio of means.