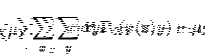- 1.
- We want
 ,
which is
,
which is
 by definition
by definition
There are three cases for which
 .
The additional law
may be used to find
.
The additional law
may be used to find
For this part of the problem, there are nine cases having X and Y both
less than or equal to 2. Add probabilities for all cases satisfying this event.
So
- 2.
- To find
 ,
sum
,
sum
 over all y values.
The result are shown here
over all y values.
The result are shown here
| x |
0 |
1 |
2 |
3 |
4 |
 |
0.180 |
0.195 |
0.250 |
0.195 |
0.180 |
To find
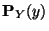 ,
add probabilities down columns
,
add probabilities down columns
| y |
0 |
1 |
2 |
3 |
4 |
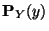 |
0.150 |
0.225 |
0.250 |
0.225 |
0.150 |
To test independence, we must see if
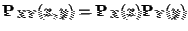 for every x and y. For x=0 and y=0
for every x and y. For x=0 and y=0
Therefore X and Y are not independent.
- 3.
- To calculate
 we must divide the joint probabilities by appropriate marginal probability for given x value. The result is conveniently shown by a table
we must divide the joint probabilities by appropriate marginal probability for given x value. The result is conveniently shown by a table
| |
y |
| x |
0 |
1 |
2 |
3 |
4 |
| 0 |
0.0556 |
0.0833 |
0.1667 |
0.4167 |
0.2778 |
| 1 |
0.1026 |
0.1538 |
0.2308 |
0.3077 |
0.2051 |
| 2 |
0.1200 |
0.1800 |
0.4000 |
0.1800 |
0.1200 |
| 3 |
0.2051 |
0.3077 |
0.2308 |
0.1538 |
0.1026 |
| 4 |
0.2778 |
0.4167 |
0.1667 |
0.0833 |
0.0556 |
If X and Y were independent, the conditional probabilities for Y would be the same. regardless of the x value. But in this exercise, the conditional probability of any particular y value changes as the x value changes. Thus X and Y are not independent.
- 4.
- The marginal probability distribution of X and Y are both symmetric around the value 2. Therefore
 .
.
Using the shortcut method for calculating variances, we square values, weight by probabilities and sum, subtracting the square of the mean at the end.
Similarly
 .
.
- 5.
- The shorter way to find
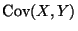 is
is
We have

From previous exercise,
 and
and

As X increases, Y tends to decrease, as shown by the negative correlation.
X and Y can't be independent, because independent random variables have 0
correlation.
- 6.
- The conditional expectation of Y given X=x is calculated like any expected value, but using conditional probabilities. That is
Similar calculations lead to the following table:
| x |
0 |
1 |
2 |
3 |
4 |
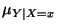 |
2.778 |
2.359 |
2.000 |
1.641 |
1.222 |
As x increases,
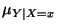 decreases, as we'd expect given that X and Y have a negative correlation.
decreases, as we'd expect given that X and Y have a negative correlation.
- 7.
- The additional law can be used to find
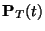 .
For example, T=X+Y=2 if
.
For example, T=X+Y=2 if
 .
Thus
.
Thus
Similar calculations yield the distribution of T
| t |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
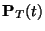 |
0.010 |
0.035 |
0.090 |
0.205 |
0.320 |
0.205 |
0.090 |
0.035 |
0.010 |
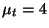 ,
by symmetry. To calculate the variance, the shortcut approach is convenient.
,
by symmetry. To calculate the variance, the shortcut approach is convenient.
We previously have found all the relevant means, variances, and
the covariance. We must have
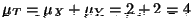 and
and