Here is a worked example to illustrate the use of the QR decomposition in solving a least squares equation.
For an ![]() matrix X, we want to find an orthogonal (length
preserving) matrix Q
(
matrix X, we want to find an orthogonal (length
preserving) matrix Q
( ![]() ) such that
) such that ![]() , where R is a block upper triangular
matrix.
, where R is a block upper triangular
matrix.
Take

then if Q is such that
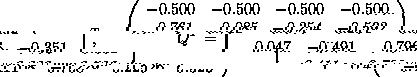
you can verify that

which is block upper triangular as required.
To solve the least squares equation
![]()
we can equivalently solve
![]()
Take for example

then
![]()

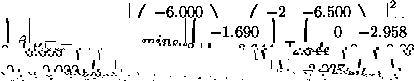
![]()
So ![]() and
and ![]() .
The residual is of length
.
The residual is of length ![]() , so that the
RMSE =
, so that the
RMSE = ![]()
Orthogonal matrix have the propery that ![]() , so that
, so that
![]() is equivalent to
is equivalent to ![]() , which is the way one usually
sees the QR decomposition.
, which is the way one usually
sees the QR decomposition.
To summarize, the objective is to decompose a matrix X as ![]() where
X is
where
X is ![]() , Q is
, Q is ![]() and R is
and R is ![]() upper
triangular, with Q orthogonal.
upper
triangular, with Q orthogonal.
The S-Plus code to produce these matrices is availble as qr.q.